1️⃣ Time Complexity : 시간 복잡도
우선 시간 복잡도를 알기 위해선 알고리즘(Algorithm) 의 개념을 이해해야 한다.
사전에 의하면 알고리즘은 수학과 컴퓨터 과학, 언어학 또는 관련된 분야에서 어떠한 문제를 해결하기 위해 정해진 일련의 절차이며, 계산을 실행하기 위한 단계적 절차를 의미한다. 즉, 문제 풀이에 필요한 계산 절차 또는 처리 과정의 순서를 말한다.
그렇다면 좋은 알고리즘, 효율적인 알고리즘은 무엇일까?
어떻게 보면 연산의 횟수와 데이터의 크기에 따른 알고리즘의 수행 시간이 적을수록 효율적인 알고리즘이라고 할 수 있다.
이를 계산하기 위한 방법이 시간 복잡도이며, 주로 'Big-O (빅-오)' 표기법을 사용한다.
이는 알고리즘의 수행 시간을 평가하는 척도라고 할 수 있다.
우리는 이를 통해 알고리즘의 성능을 예측해볼 수 있다.
시간 복잡도를 나타내는 방법에는 대표적으로 세가지 방법이 있다.
- Ω (Big-Omega) : 빅-오메가 표기법
- 최선의 경우 알고리즘의 수행 시간이 최소 이만큼 걸린다. (Best Case)
- 점근적 하한 표기이다.
- θ (Big-Theta) : 빅-세타 표기법
- 일반적인 경우 알고리즘의 평균 수행 시간을 나타낸다. (Average Case)
- Ω 와 O 표기가 같을 때 사용한다.
- O (Big-O) : 빅-오 표기법
- 최악의 경우 알고리즘의 수행 시간이 최대 이만큼 걸린다. (Worst Case)
- 점근적 상한 표기이다.
위 세 가지 방법 중 실제로 시간 복잡도를 나타낼 때엔 'Big-O' 표기법으로 나타낸다.
만약 연산의 횟수가 다항식으로 표현된다면, 최고차항만 나타내는 방식이다.
예를 들어 데이터의 크기가 n 이라고 가정할 때,
- T(𝑛) = 𝑛² + 3𝑛 + 2 = O(𝑛²)
- T(𝑛) = 5𝑛 + 6 = O(𝑛)
- T(𝑛) = 3 = O(1)
로 나타낼 수 있다.
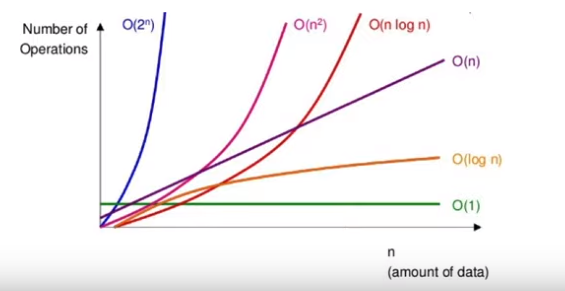
또한 Big-O 표기법의 종류는 다음과 같다.
- O(1)
- O(log n)
- O(n)
- O(n log n)
- O(n²)
- O(2ᴺ)
2️⃣ O(1) : 상수 시간 (Constant Time)
이는 입력 데이터의 크기에 상관 없이 일정한 연산을 수행한다.
즉, 입력 데이터가 늘어나도 시간이 늘어나지 않는다.
public class Main(){
public static int plus(int a,int b){
return a+b;
}
public static void main(String[] args){
int result=plus(1,2);
System.out.print(result);
}
}
main 메소드에서 plus 함수를 한 번 시행하여 a+b 를 return 받은 것이 전부이므로, 항상 일정하다.
따라서 T(n) = O(1) 이다.
3️⃣ O(logN) : 로그 시간 (Logarithmic Time)
컴퓨터는 이진수 시스템을 사용하기 때문에, 로그의 밑을 대부분 2로 사용한다.
그러나 로그 시간에서는 로그의 밑과 상관 없이 logN 이 로그 시간 알고리즘의 표준 표기법이 된다.
대표적인 예로는 이진 트리에서의 연산 또는 이진 탐색에서 찾아볼 수 있다.
이는 로그의 성질에 의해 데이터가 두 배로 증가할 때마다 한 단계씩 늘어나는 알고리즘이다.
즉, 입력 데이터의 크기가 커질 때, 연산 횟수가 logN 에 비례해서 증가한다.
public class Main{
public static void main(String[] args){
for(int i=0;i<n;i*2){
System.out.print(i);
}
}
}따라서 T(n) = O(log n) 이다.
4️⃣ O(N) : 선형 시간 (Linear Time)
입력 데이터의 크기(N) 가 커짐에 따라 연산 횟수가 N에 비례하여 증가하는 선형적인 형태이다.
대표적으로 n 번 반복하는 for 문을 예시로 들 수 있다.
public class Main{
public static void main(String[] args){
for(int i=0;i<n;i++){
System.out.println(i);
}
}
}따라서 T(n) = O(n) 이다.
5️⃣ O(N^2) : 2차 시간 (Quadratic Time)
입력 데이터의 크기(N) 가 커짐에 따라 연산 횟수가 제곱에 비례하여 증가하는 형태이다.
대표적으로 이중 for문이 있다. 수가 커짐에 따라 지수의 영향력이 줄어 N^3, N^4 ... 모두 O(N^2) 이다.
public class Main{
public static void main(String[] args){
for(int i=0;i<10;i++){
for(int j=0;j<10;j++){
System.out.println(i+" "+j);
}
}
}
}따라서 T(n) = O(n^2) 이다.
6️⃣ O(2^N) : 지수 시간 (Exponential Time)
입력 데이터의 크기(N) 가 커짐에 따라 연산 횟수가 지수(2^N) 에 비례하여 증가하는 형태이다.
지금까지 소개한 방법 중 가장 시간이 오래 걸린다.
대표적인 예로는 재귀를 통해 피보나치 수를 구하는 알고리즘이 있다.
int fibonacci (int num) {
if (num <= 1)
return num;
return fibonacci(n-1) + fibonacci(n-2);
}1️⃣ Time Complexity : 시간 복잡도
우선 시간 복잡도를 알기 위해선 알고리즘(Algorithm) 의 개념을 이해해야 한다.
사전에 의하면 알고리즘은 수학과 컴퓨터 과학, 언어학 또는 관련된 분야에서 어떠한 문제를 해결하기 위해 정해진 일련의 절차이며, 계산을 실행하기 위한 단계적 절차를 의미한다. 즉, 문제 풀이에 필요한 계산 절차 또는 처리 과정의 순서를 말한다.
그렇다면 좋은 알고리즘, 효율적인 알고리즘은 무엇일까?
어떻게 보면 연산의 횟수와 데이터의 크기에 따른 알고리즘의 수행 시간이 적을수록 효율적인 알고리즘이라고 할 수 있다.
이를 계산하기 위한 방법이 시간 복잡도이며, 주로 'Big-O (빅-오)' 표기법을 사용한다.
이는 알고리즘의 수행 시간을 평가하는 척도라고 할 수 있다.
우리는 이를 통해 알고리즘의 성능을 예측해볼 수 있다.
시간 복잡도를 나타내는 방법에는 대표적으로 세가지 방법이 있다.
- Ω (Big-Omega) : 빅-오메가 표기법
- 최선의 경우 알고리즘의 수행 시간이 최소 이만큼 걸린다. (Best Case)
- 점근적 하한 표기이다.
- θ (Big-Theta) : 빅-세타 표기법
- 일반적인 경우 알고리즘의 평균 수행 시간을 나타낸다. (Average Case)
- Ω 와 O 표기가 같을 때 사용한다.
- O (Big-O) : 빅-오 표기법
- 최악의 경우 알고리즘의 수행 시간이 최대 이만큼 걸린다. (Worst Case)
- 점근적 상한 표기이다.
위 세 가지 방법 중 실제로 시간 복잡도를 나타낼 때엔 'Big-O' 표기법으로 나타낸다.
만약 연산의 횟수가 다항식으로 표현된다면, 최고차항만 나타내는 방식이다.
예를 들어 데이터의 크기가 n 이라고 가정할 때,
- T(𝑛) = 𝑛² + 3𝑛 + 2 = O(𝑛²)
- T(𝑛) = 5𝑛 + 6 = O(𝑛)
- T(𝑛) = 3 = O(1)
로 나타낼 수 있다.
또한 Big-O 표기법의 종류는 다음과 같다.
- O(1)
- O(log n)
- O(n)
- O(n log n)
- O(n²)
- O(2ᴺ)

2️⃣ O(1) : 상수 시간 (Constant Time)
이는 입력 데이터의 크기에 상관 없이 일정한 연산을 수행한다.
즉, 입력 데이터가 늘어나도 시간이 늘어나지 않는다.
public class Main(){
public static int plus(int a,int b){
return a+b;
}
public static void main(String[] args){
int result=plus(1,2);
System.out.print(result);
}
}
main 메소드에서 plus 함수를 한 번 시행하여 a+b 를 return 받은 것이 전부이므로, 항상 일정하다.
따라서 T(n) = O(1) 이다.
3️⃣ O(logN) : 로그 시간 (Logarithmic Time)
컴퓨터는 이진수 시스템을 사용하기 때문에, 로그의 밑을 대부분 2로 사용한다.
그러나 로그 시간에서는 로그의 밑과 상관 없이 logN 이 로그 시간 알고리즘의 표준 표기법이 된다.
대표적인 예로는 이진 트리에서의 연산 또는 이진 탐색에서 찾아볼 수 있다.
이는 로그의 성질에 의해 데이터가 두 배로 증가할 때마다 한 단계씩 늘어나는 알고리즘이다.
즉, 입력 데이터의 크기가 커질 때, 연산 횟수가 logN 에 비례해서 증가한다.
public class Main{
public static void main(String[] args){
for(int i=0;i<n;i*2){
System.out.print(i);
}
}
}따라서 T(n) = O(log n) 이다.
4️⃣ O(N) : 선형 시간 (Linear Time)
입력 데이터의 크기(N) 가 커짐에 따라 연산 횟수가 N에 비례하여 증가하는 선형적인 형태이다.
대표적으로 n 번 반복하는 for 문을 예시로 들 수 있다.
public class Main{
public static void main(String[] args){
for(int i=0;i<n;i++){
System.out.println(i);
}
}
}따라서 T(n) = O(n) 이다.
5️⃣ O(N^2) : 2차 시간 (Quadratic Time)
입력 데이터의 크기(N) 가 커짐에 따라 연산 횟수가 제곱에 비례하여 증가하는 형태이다.
대표적으로 이중 for문이 있다. 수가 커짐에 따라 지수의 영향력이 줄어 N^3, N^4 ... 모두 O(N^2) 이다.
public class Main{
public static void main(String[] args){
for(int i=0;i<10;i++){
for(int j=0;j<10;j++){
System.out.println(i+" "+j);
}
}
}
}따라서 T(n) = O(n^2) 이다.
6️⃣ O(2^N) : 지수 시간 (Exponential Time)
입력 데이터의 크기(N) 가 커짐에 따라 연산 횟수가 지수(2^N) 에 비례하여 증가하는 형태이다.
지금까지 소개한 방법 중 가장 시간이 오래 걸린다.
대표적인 예로는 재귀를 통해 피보나치 수를 구하는 알고리즘이 있다.
int fibonacci (int num) {
if (num <= 1)
return num;
return fibonacci(n-1) + fibonacci(n-2);
}