DFS (Depth - First Search)
깊이 우선 탐색 (DFS) 는 그래프 탐색 기법 중 하나이다.
간단히 그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기의 최대 깊이까지 탐색 후, 다른 분기로 이동한 뒤 탐색을 수행하는 알고리즘이다.
| 기능 | 특징 | 시간 복잡도 (노드 수:V , 에지 수:E) |
| 그래프 완전 탐색 | 1. 재귀 함수로 구현 2. 스택 자료 구조 이용 |
O(V + E) |
DFS 는 크게 두 가지 방법으로 구현할 수 있다.
1. 재귀 함수
2. 스택
나는 두 방법 중 재귀 함수로 구현을 많이 한다. 사실은 재귀 함수 또한 스택의 성질인 후입선출(FIFO)을 갖는다.
또한 DFS 는 한 번 방문한 노드를 재방문하면 안되기에 이를 체크해주는 배열이 필요하다.
이제 예시를 보자.
아래와 같은 그래프가 있다고 하자. 여기선 쉬운 설명을 위해 스택을 사용하겠다.

[ 시작 노드를 정한 뒤 인접 리스트를 초기화 ]
DFS를 위한 초기 작업은 다음과 같다.
1. 인접 리스트로 그래프 표현
2. 방문 배열 초기화
3. 시작 노드를 스택에 삽입
만약 시작 노드가 1이라면 인접 리스트는 다음과 같을 것이다.

다음으로 방문 배열과 스택의 초기 상태는 아래와 같을 것이다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| T | F | F | F | F | F |
[ 방문 배열 ]

[ 탐색 ]
DFS로 탐색하는 알고리즘은 다음과 같다.
1. 스택에서 노드를 꺼내면서 탐색 순서에 꺼낸 노드를 기록
2. 해당 노드의 인접 노드를 스택에 삽입
3. 스택에 삽입된 노드를 방문 배열에서 체크
위의 예시에서 처음 스택에 삽입된 노드는 '1' 이다.
스택에서 가장 위에 있는 노드 '1'을 꺼내면서 탐색 순서에 기록한다.
즉, 탐색 순서는 1 -> 이 된다.
다음으로 노드 '1'의 인접 노드인 노드 '2', '5' 을 스택에 삽입한다.
또한 방문 배열에서 노드 '2' , '5' 에 대한 값을 'T' 로 바꿔준다.
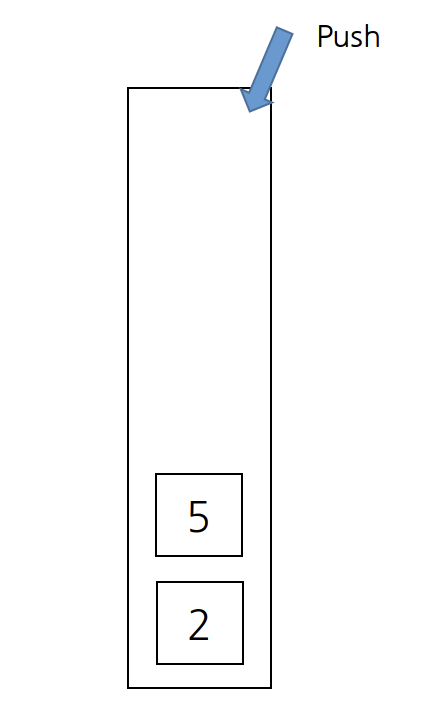
위 작업을 한 번 반복하면 스택에는 차례대로 2, 5 가 있다.
방문 배열과 스택은 아래와 같다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| T | T | F | F | T | F |
[ 방문 배열 ]
다음 반복을 위해 스택에서 pop을 하면 노드 '5'가 나올 것이다.
그러면 탐색 순서는 1 -> 5 -> 가 된다.
노드 '5'의 인접 노드인 노드 '1', '2', '4' 를 스택에 삽입해야 한다.
그런데 노드 '1'과 '2'는 이미 방문하였으므로 노드 '4' 만 스택에 삽입한다.
이후 방문 배열에서 노드 '4' 에 대한 값을 'T' 로 바꿔준다.
이런 식으로 스택에 값이 없을 때까지 위 과정을 반복하게 된다.
[ 코드 ]
이제 예시로 주어진 그래프를 시작 노드를 '1' 로 정하고 DFS를 수행하는 코드를 작성해보자.
1️⃣ 스택으로 구현한 DFS
public class Main{
static List<Integer>[] list; // 인접 리스트
static boolean[] visited; // 방문 배열
private static void DFS(int node) {
Stack<Integer> stack = new Stack<>();
stack.push(node);
visited[node] = true;
while(!stack.isEmpty()) {
int now = stack.pop();
System.out.print(now + " -> ");
for(int next : list[now]) {
if(!visited[next]) {
stack.push(next);
visited[next] = true;
}
}
}
}
public static void main(String[] args) {
list = new ArrayList[7];
visited = new boolean[7];
for(int i=1;i<7;i++)
list[i] = new ArrayList<>();
list[1].add(2);
list[1].add(5);
list[2].add(1);
list[2].add(3);
list[2].add(5);
list[3].add(2);
list[3].add(4);
list[4].add(3);
list[4].add(5);
list[4].add(6);
list[5].add(1);
list[5].add(2);
list[5].add(4);
list[6].add(4);
DFS(1);
}
}
결과 :
1 -> 5 -> 4 -> 6 -> 3 -> 2 ->
2️⃣ 재귀로 구현한 DFS
public class Main{
static List<Integer>[] list; // 인접 리스트
static boolean[] visited; // 방문 배열
private static void DFS(int node) {
visited[node] = true;
System.out.print(node + " -> ");
for(int now : list[node]) {
if(!visited[now])
DFS(now);
}
}
public static void main(String[] args) {
list = new ArrayList[7];
visited = new boolean[7];
for(int i=1;i<7;i++)
list[i] = new ArrayList<>();
list[1].add(2);
list[1].add(5);
list[2].add(1);
list[2].add(3);
list[2].add(5);
list[3].add(2);
list[3].add(4);
list[4].add(3);
list[4].add(5);
list[4].add(6);
list[5].add(1);
list[5].add(2);
list[5].add(4);
list[6].add(4);
DFS(1);
}
}
결과 :
1 -> 2 -> 3 -> 4 -> 5 -> 6 ->
코드를 보면 알 수 있듯 재귀로 구현한 코드가 훨씬 짧고 간결하기 때문에 재귀를 자주 이용한다.
