https://www.acmicpc.net/problem/18870
18870번: 좌표 압축
수직선 위에 N개의 좌표 X1, X2, ..., XN이 있다. 이 좌표에 좌표 압축을 적용하려고 한다. Xi를 좌표 압축한 결과 X'i의 값은 Xi > Xj를 만족하는 서로 다른 좌표의 개수와 같아야 한다. X1, X2, ..., XN에 좌
www.acmicpc.net

1) 문제
수직선 위에 N개의 좌표 X1, X2, ..., XN이 있다. 이 좌표에 좌표 압축을 적용하려고 한다.
Xi를 좌표 압축한 결과 X'i의 값은 Xi > Xj를 만족하는 서로 다른 좌표의 개수와 같아야 한다.
X1, X2, ..., XN에 좌표 압축을 적용한 결과 X'1, X'2, ..., X'N를 출력해보자.
2) 입력
첫째 줄에 N이 주어진다.
둘째 줄에는 공백 한 칸으로 구분된 X1, X2, ..., XN이 주어진다.
3) 출력
첫째 줄에 X'1, X'2, ..., X'N을 공백 한 칸으로 구분해서 출력한다.
4) 제한
- 1 ≤ N ≤ 1,000,000
- -10^9 ≤ Xi ≤ 10^9
예제 입력

[접근 방법]
1. 벡터 v1, v2 를 만든다. 처음 v1은 좌표를 입력받고 v2=v1 로 복사해준다.
2. v1을 sort 하고 'erase' , 'unique' 를 이용하여 중복된 원소까지 모두 제거해준다.
3. v2의 원소를 차례대로 idx 라는 변수에 저장하고 v1에서 몇번째 원소인지 반환한다.
4. 벡터의 인덱스는 0부터 시작하므로 'lower_bound' 를 이용하면 자신의 위치가 몇번째인지 알게된다.
5. v1에서 찾으려는 위치는 자신보다 작은 원소의 갯수와 같다.
이 문제의 조건을 잘 살펴보자. 처음 보면 헷갈릴 수도 있다.
" Xi를 좌표 압축한 결과 X'i의 값은 Xi > Xj를 만족하는 서로 다른 좌표의 개수 " 라는 말이 중요 포인트다.
즉, Xi 대신 Xi 보다 작은 원소가 몇개 있는지 구하라는 말이다.
하지만 무턱대고 구하면 안된다. 중복된 원소는 한번만 세기 때문이다.
[ 개념 ]
여기서 'lower_bound' 라는 개념을 이용하면 좋다. 'lower_bound' 가 무엇인지 살짝 알아보자.
이는 찾으려는 key 값보다 같거나 큰 숫자가 배열 몇 번째에서 처음 등장하는지 찾기 위한 함수이다.
단, 사용하기 위해선 오름차순 정렬이 되어있어야 한다.
쉽게 예를 들어보겠다. v={ 1,2,3,4,5 } 가 있다.
lower_bound(2) 는 2보다 크거나 같은 숫자가 몇 번째 위치에 있는지를 나타내므로 3의 위치라고 할 수 있다.
벡터의 인덱스는 0부터 시작하므로 3의 위치인 2를 반환한다.
하지만 lower_bound 의 반환값은 iterator 이므로 실제 인덱스값을 추출하려면 v의 첫 번째 주소를 빼주면 된다.
사용법은 다음과 같다.
lower_bound(v.begin(),v.end(),key)-v.begin()
'lower_bound' 와 비슷하게 'upper_bound' 는 '이상' 이 아닌 '초과' 하는 값을 찾는 함수이다. 똑같이 응용 가능하다.
그럼 이 함수를 문제를 풀 때 어떻게 활용하는지 코드와 함께 알아보겠다.
[코드 설명]
이번 문제엔 제한 조건이 있었다.
- 1 ≤ N ≤ 1,000,000
- -10^9 ≤ Xi ≤ 10^9
혹시 모르니 입출력 받는 속도를 높이기 위해 코드 하나를 추가했다. 자세한 설명은 다음에 하겠다.
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
이후 벡터 v1, v2 를 만들어 주고 v1에 좌표를 입력받는다.
v2=v1 을 통해 v2 를 v1과 같게 복사해준다.
이제 v1을 오름차순 정렬하고 중복된 원소도 제거해준다.
sort(v1.begin(), v1.end());
v1.erase(unique(v1.begin(), v1.end()), v1.end());
현재 v2 는 정렬 전 v1 과 같은 상태이므로 v2의 원소를 하나씩 뽑아 자신보다 작은 숫자가 몇개인지 세면 된다.
위 예제를 통해 어떤 원리인지 알아보겠다.
v1={-10, -9, 2, 4}
v2={2, 4, -10, 4, -9}
v2 의 첫 번째 원소 2를 key값으로 설정한다.
v1 에서 2 는 인덱스상 2번째에 위치한다. (lower_bound 이므로 자신과 같은 값의 위치부터 반환한다.)
두 번째 원소인 4를 key값으로 하면 역시 인덱스상 3번째이다.
여기서 중요한 점은 인덱스값이 key값보다 작은 원소의 갯수와 같다는 것이다.
따라서 이 'lower_bound' 값을 그대로 출력해주면 정답이 된다.
for (int x : v2) {
int idx = lower_bound(v1.begin(), v1.end(), x) - v1.begin();
cout << idx << " ";
}
정답을 도출하는 코드이다. 정수 x 를 v2로부터 하나씩 뽑아 lower_bound 의 key값으로 넣어준다는 의미이다.
이후 idx에 저장하고 이를 그대로 출력해주면 답이 나온다. 실행해보자.

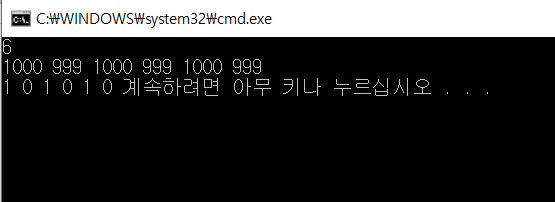
정답이 잘 나왔다.
[ 최종 코드 ]
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main(void) {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
vector <int> v1(N);
vector <int> v2(N);
for (int i = 0; i < N; i++)
cin >> v1[i];
v2 = v1;
sort(v1.begin(), v1.end());
v1.erase(unique(v1.begin(), v1.end()), v1.end());
for (int x : v2) {
int idx = lower_bound(v1.begin(), v1.end(), x) - v1.begin();
cout << idx << " ";
}
}[느낀점]
이번 문제는 꽤 간단해보이지만 풀다가 계속 헷갈렸다.
중복된 원소를 세지 않는다는 조건때문에 감이 잘 안잡혔다.
전에 'lower_bound' , 'upper_bound' 에 대해 공부 한 적이 있었지만 가물가물해서 다시 찾아봤다.
보통 이렇게 몇 번째 위치에 있는 원소를 알아낼 때 유용한 함수라고 생각한다.
이외에도 중복된 원소는 몇개인지 등 활용가능한 문제는 많다.
이번에 정렬 공부하면서 아직 멀었다고 느꼈다.